09-CG-Clipping
Clipping
Eliminate portions of objects outside the viewing frustum
View Frustum
- boundaries of the image plane projected in 3D
- a near & far clipping plane
User may define additional clipping planes
Why Clip?
- Avoid degeneracies
- Don’t draw stuff behind the eye
- Avoid division by 0 and overflow
- Efficiency
- Other graphics applications (often non-convex)
Clipping Strategies
Don't clip (and hope for the best)
完全不进行裁剪,直接渲染所有物体,依赖后续阶段(如光栅化或深度测试)处理不可见部分。
优缺点:
- 优点:实现简单,无需额外计算。
- 缺点:
- 效率极低:浪费资源渲染不可见物体。
- 可能引发错误:如近平面内物体导致投影失真(透视除法分母趋近于0)。
适用场景:
- 极简单场景或调试阶段(如仅测试少量图元)。
Clip on-the-fly during rasterization
在光栅化阶段(即生成像素时)实时判断像素是否在视锥体内,仅绘制可见像素。
优缺点:
- 优点:
- 无需提前处理几何,逻辑简单。
- 适用于动态变化的裁剪区域(如实时调整的裁剪框)。
- 缺点:
- 所有几何(包括完全不可见的)仍需经过顶点变换、光照等阶段,效率仍有浪费。
- 对复杂模型(如高多边形网格)性能影响显著。
- 优点:
适用场景:
- 2D图形或简单3D场景(如手机游戏中的轻量级渲染)。
Analytical clipping: alter input geometry
在几何处理阶段(如顶点着色器后),通过数学分析提前裁剪掉视锥体外的部分,修改输入几何(如截断线段、分割多边形)。
典型算法:
- 线段裁剪:Sutherland-Hodgman算法(逐平面裁剪线段,保留可见部分)。
- 多边形裁剪:Weiler-Atherton算法(处理复杂多边形的裁剪与重建)。
优缺点:
- 优点:
- 高效:提前剔除不可见几何,减少后续阶段(如光栅化、片元着色)的工作量。
- 精确:几何级裁剪,避免像素级冗余计算。
- 缺点:
- 实现复杂:需处理几何求交(如线段与平面交点、多边形分割)。
- 依赖几何类型:对非多边形图元(如曲线)处理困难。
- 优点:
适用场景:
- 主流3D渲染管线(如游戏引擎、CAD软件),是图形流水线的标准阶段。
Point & Line Clipping
Implicit 3D Plane Equation
Plane defined by:
- point
& normal - normal
& offset - 3 points
Implicit plane equation
Homogeneous Coordinates
Homogenous point:
- infinite number of equivalent homogenous coordinates:
Homogenous Plane Equation:
Infinite number of equivalent plane expressions:
Point-to-Plane Distance
If
d is a signed distance
- If
pass through - If
clip
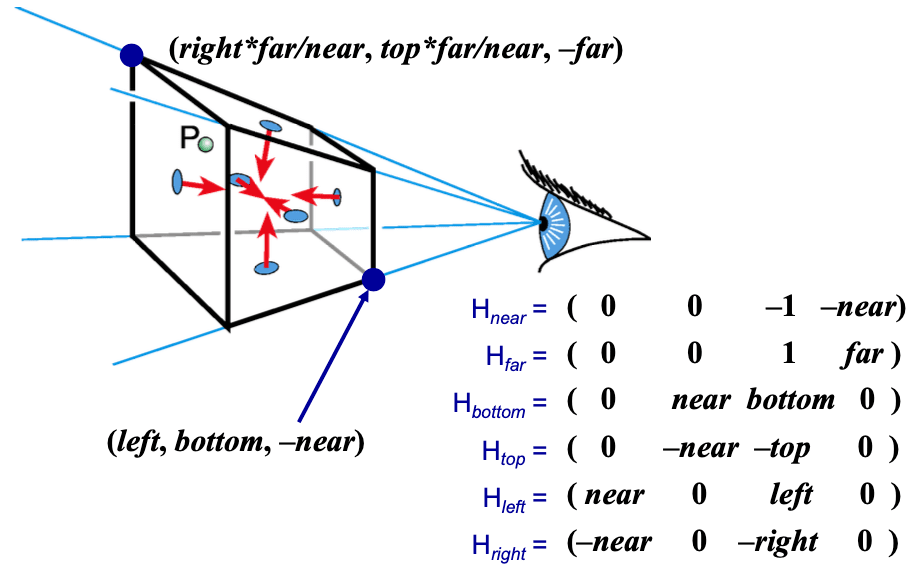
Clipping with respect to View Frustum
Test against each of the 6 planes
- Normals oriented towards the interior
Clip point
if any
Clipping & Transformation
Transform M (e.g. from world space to NDC) 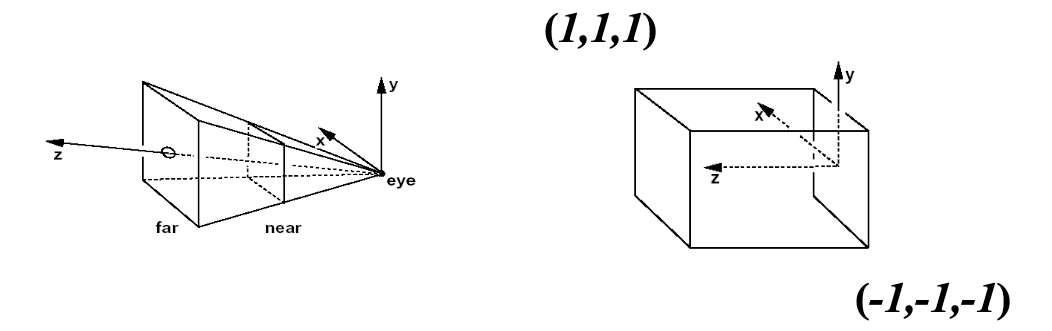
Role of Transformation Matrix
represents a composite transformation (e.g., model → view → projection) that maps vertices from world space to clip space (or NDC, normalized device coordinates). - Example:
.
Transformation of Points vs. Planes
- Points/Vertices: Transformed directly by
: - Clipping Planes: Plane equations (e.g., view frustum planes) cannot be transformed with
directly. Instead, they require the inverse transpose matrix to preserve their geometric relationship with points.
Mathematical Reason: Duality of Points and Planes
- A plane
and a point satisfy (point lies on plane). - After transformation, we need
to imply . This leads to:
The inverse undoes the effect of
Practical Example: View Frustum to NDC
- View frustum planes (defined in view space) are transformed to NDC using
, where is the projection matrix. - This ensures that the clipping condition (e.g.,
for interior points) remains valid in the new coordinate space (e.g., NDC’s cube).
Line Segment Clipping (4 cases)
If
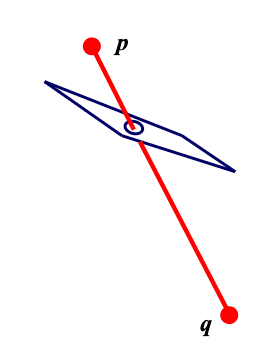
- clip q to plane
If
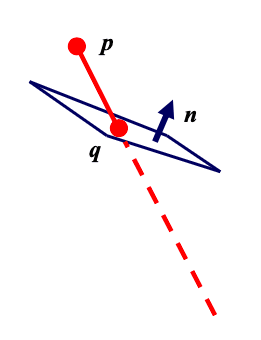
- clip p to plane
If
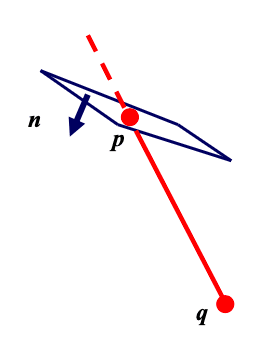
- pass through
If
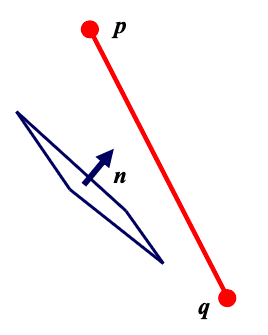
- clipped out
Line – Plane Intersection
Explicit (Parametric) Line Equation
How do we intersect?
Insert explicit equation of line into implicit equation of plane:
Line Parametric Equation: A line through points
and is , where (or for a segment). Plane Implicit Equation: A plane with normal vector
is . Intersection Calculation:
- Substitute
into the plane equation to solve for : - If
, the line intersects the plane at .
- Substitute
Validity for Segments:
- For a line segment, check if
.
- For a line segment, check if
Graphics Application:
- Use
to interpolate attributes (color, normals) at the intersection point for rendering/clipping.
- Use
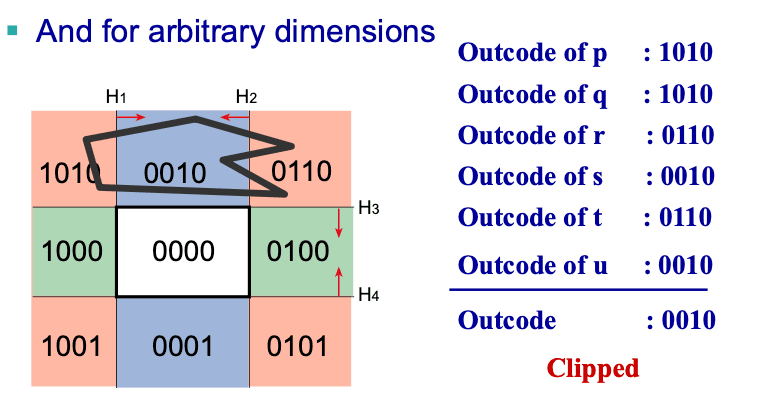
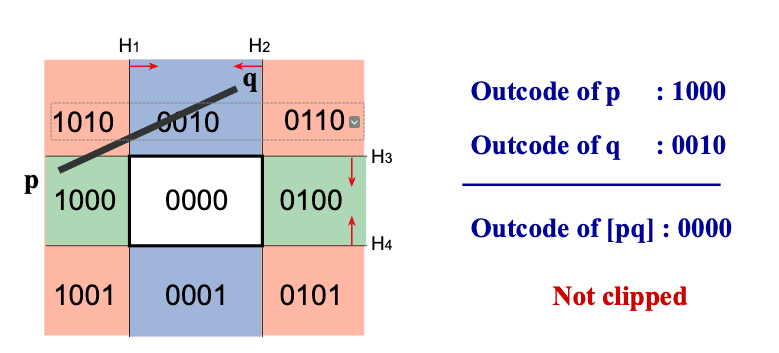
Acceleration using outcodes
Efficiency Problem:
- The computation of the intersections, and any corresponding interpolated values is unnecessary
Improve Efficiency: Outcode
Compute the sidedness of each vertex with respect to each bounding plane (0 = valid)
Combine into binary outcode using logical AND
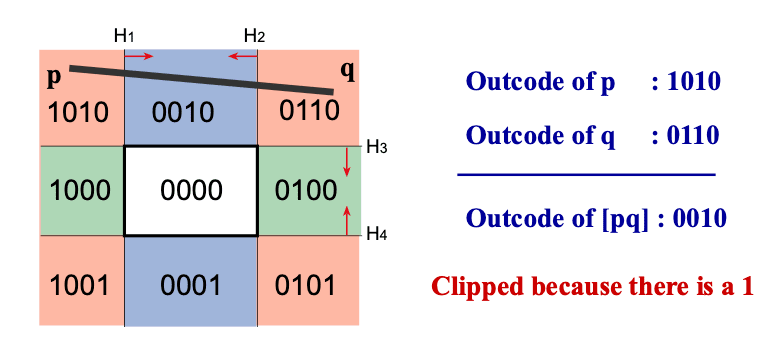
- Outcodes的优势仅体现在完全不可见线段的快速剔除,可节省大量无效计算;
- 比如
- 比如
- 对于部分可见或完全可见线段,计算量与传统方法相当,无法进一步优化。
- 比如
- 比如